
In his 1202 treatise, Book of Calculation, Fibonacci described the numerical sequence that now bears his name: 1, 2, 3, 5, 8, 13, 21. The person most closely associated with the Fibonacci sequence is the 13th-century mathematician Leonardo Pisano his nickname was "filius Bonacci" ( son of Bonacci), which got shortened to Fibonacci. The branched tips, called meristems, make up a logarithmic spiral, and the number of spirals on the head of Romanesco cauliflower is a Fibonacci number, which in turn is related to what's known as the " golden ratio."
#FIBONACCI GOLDENRATIO SERIES#
Many fractal patterns exist only in mathematical theory, but over the last few decades, scientists have found there are fractal aspects to many irregular yet patterned shapes in nature, such as the branchings of rivers and trees-or the strange self-similar repeating buds that make up the Romanesco cauliflower.Įach bud is made up of a series of smaller buds, although the pattern doesn't continue down to infinitely smaller size scales, so it's only an approximate fractal. For that reason, fractals are often likened to Russian nesting dolls. That single geometric pattern repeats thousands of times at different magnifications (self-similarity). Now, a team of French scientists from the CNRS has identified the underlying mechanism that gives rise to this unusual pattern, according to a new paper published in Science.įractal geometry is the mathematical offspring of chaos theory a fractal is the pattern left behind in the wave of chaotic activity. This self-similarity is particularly notable in the Romanesco variety because of the distinctive conical shape of its florets. Cauliflower provides a unique example of this phenomenon, because those spirals repeat at several different size scales-a hallmark of fractal geometry.
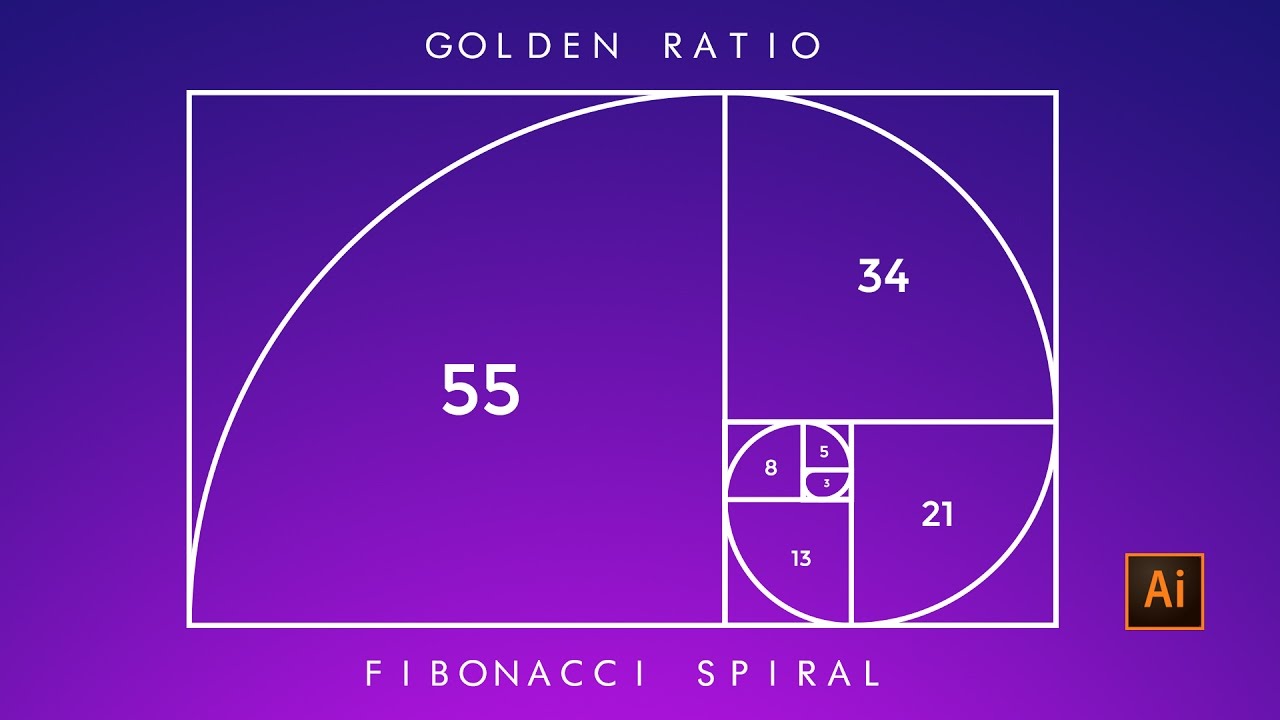

It has long been observed that many plants produce leaves, shoots, or flowers in spiral patterns.


 0 kommentar(er)
0 kommentar(er)
